Single Pendulum Simulator (April 2024)

Single Pendulum Simulations comparing Euler's Method, Heun's Method, RK4, and Dormand-Prince.

In 10th grade, when I was self studying AP Physics 1, I became intrigued by the motion of double pendulums. After watching a Youtube video [1] by Action Lab, I decided it would be interesting to simulate a double pendulum using Python. I got the inspiration for this project from myphysicslab.com [2], which includes a variety of interesting physics simulations where the user can adjust parameters. These simulations are programmed using TypeScript, and I decided to create the same simulations in Python. However, as I worked on this program, I realized how difficult it was. I decided that I need to simulate a single pendulum first.

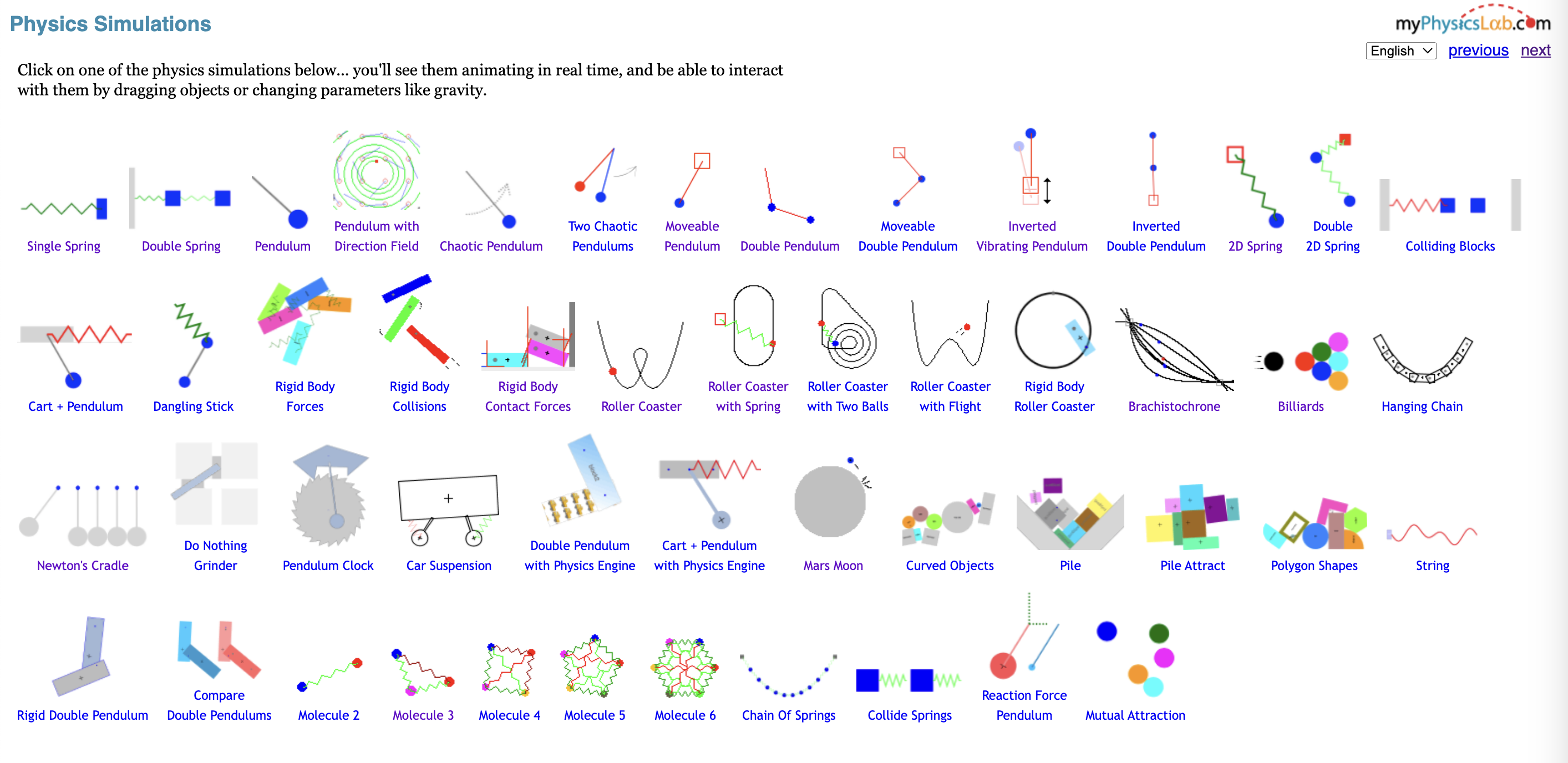
According to myphysicslab.com [2], "the heart of a physics simulation is the set of differential equations that describe how the variables evolve over time". This aligned well with my the Differential Equations class I had taken this year. I decided to test different methods for solving these differential equations.

myphysicslab.com [2] allows the user to choose between a few options for the simulation. 3 options included are Euler's Method, Modified Euler (Heun's Method), and Runge-Kutta (RK4).

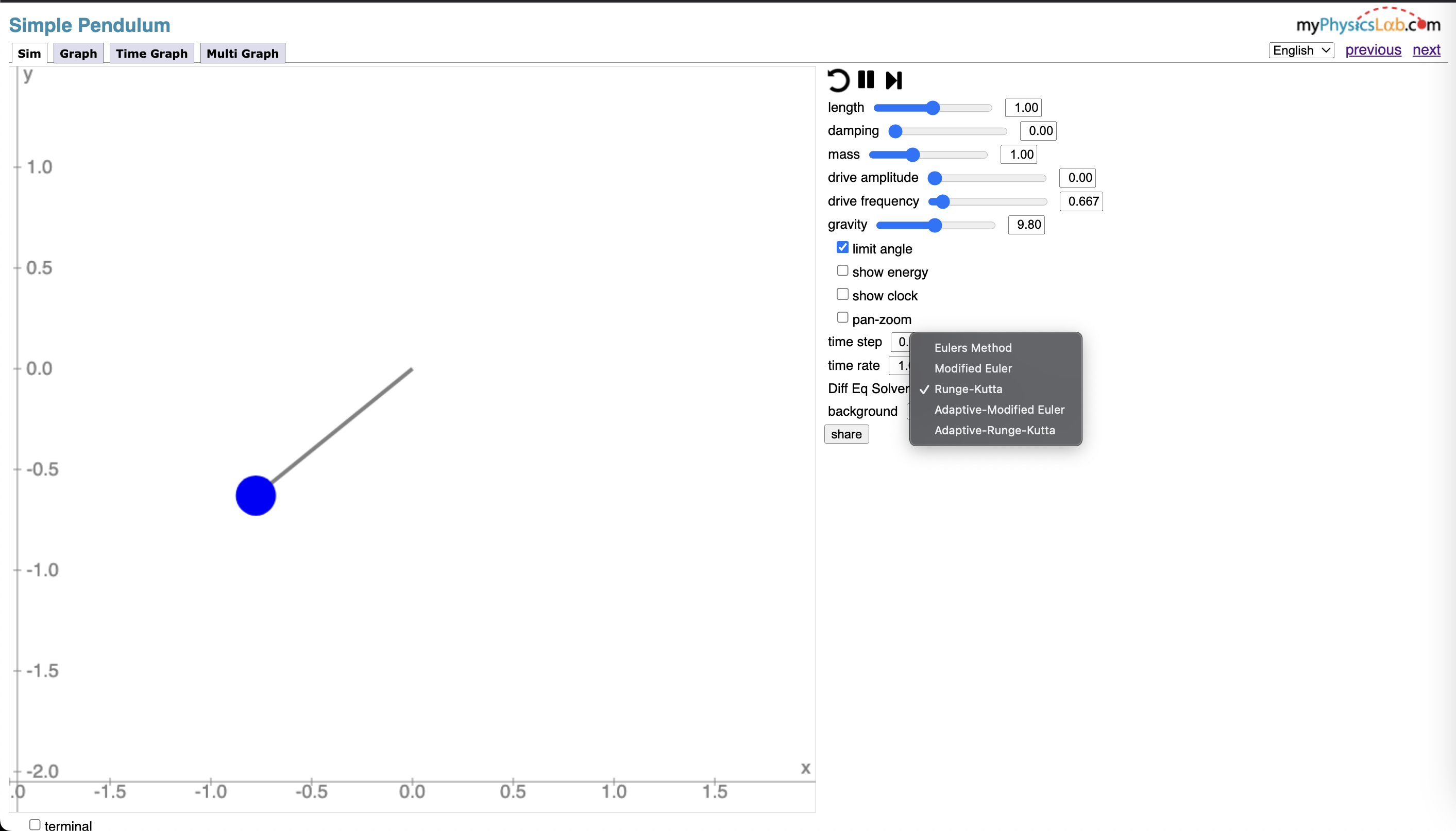
Through my independent research of additional methods, I came across the Dormand-Prince Method. This was not taught my course's curriculum, and it took time to fully understand it. After watching a Youtube video [3] and learning more about Dormand-Prince online, I decided to implement it. This took a long time due to the large number of coefficients needed and all the equations I had to solve.

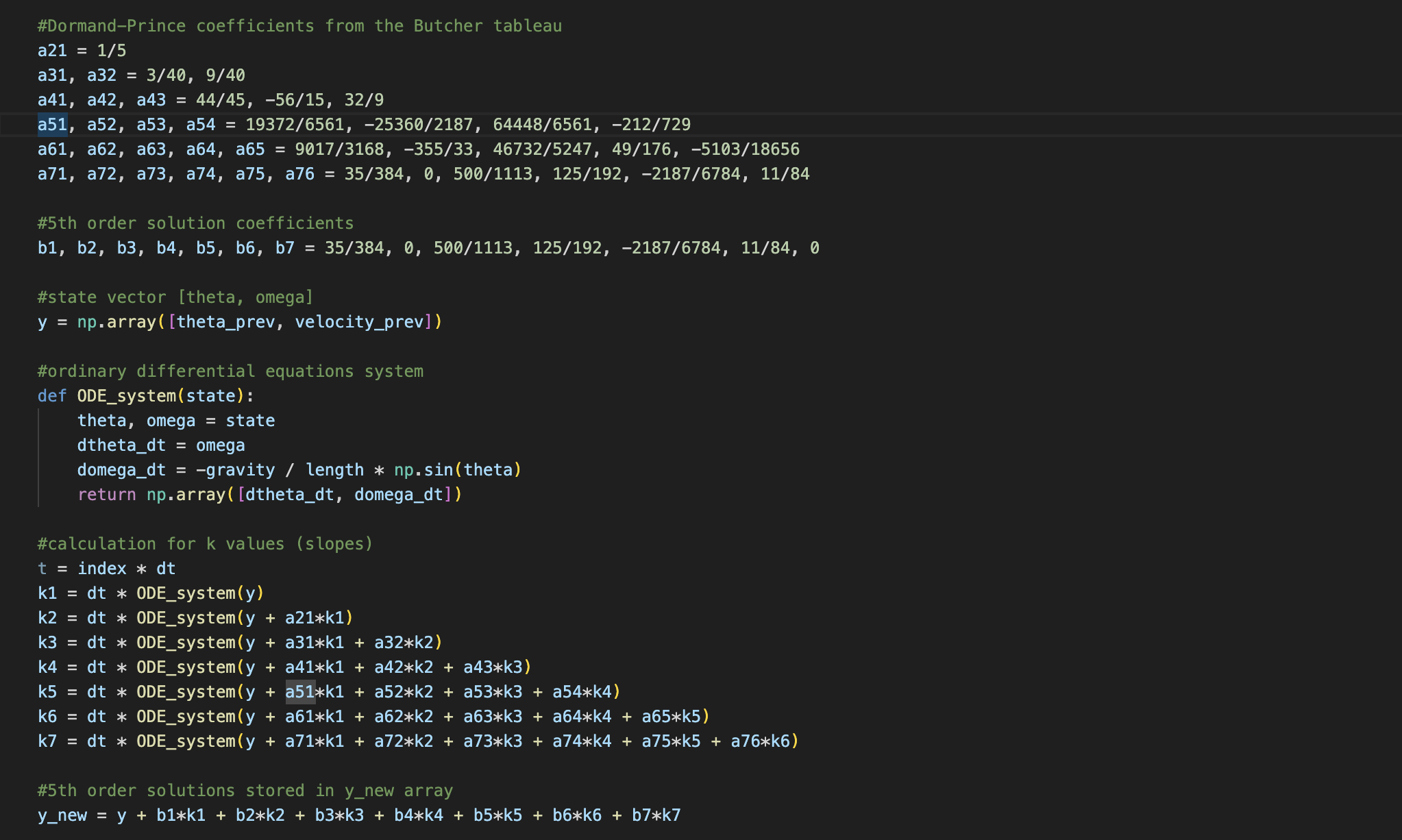
Conclusion

This project was both fun and educational. I was able to learn a lot about Dormand-Prince and its applications. I was also able to improve my proficiency with the Matplotlib The most satisfying part was comparing the four methods I used: Euler's, Heun's, RK4, and lastly Dormand-Prince. The accuracy of each program increased in that order. I calculated error as the total mechanical energy in each frame compared to the initial total mechanical energy. Only when using very large values for gravity (g) and mass (m) will the accuracy difference between RK4 and Dormand-Prince show. The image below shows how little error Dormand-Prince accumulutes despite large values of mass = 1000kg and gravity = 100m/s^2.

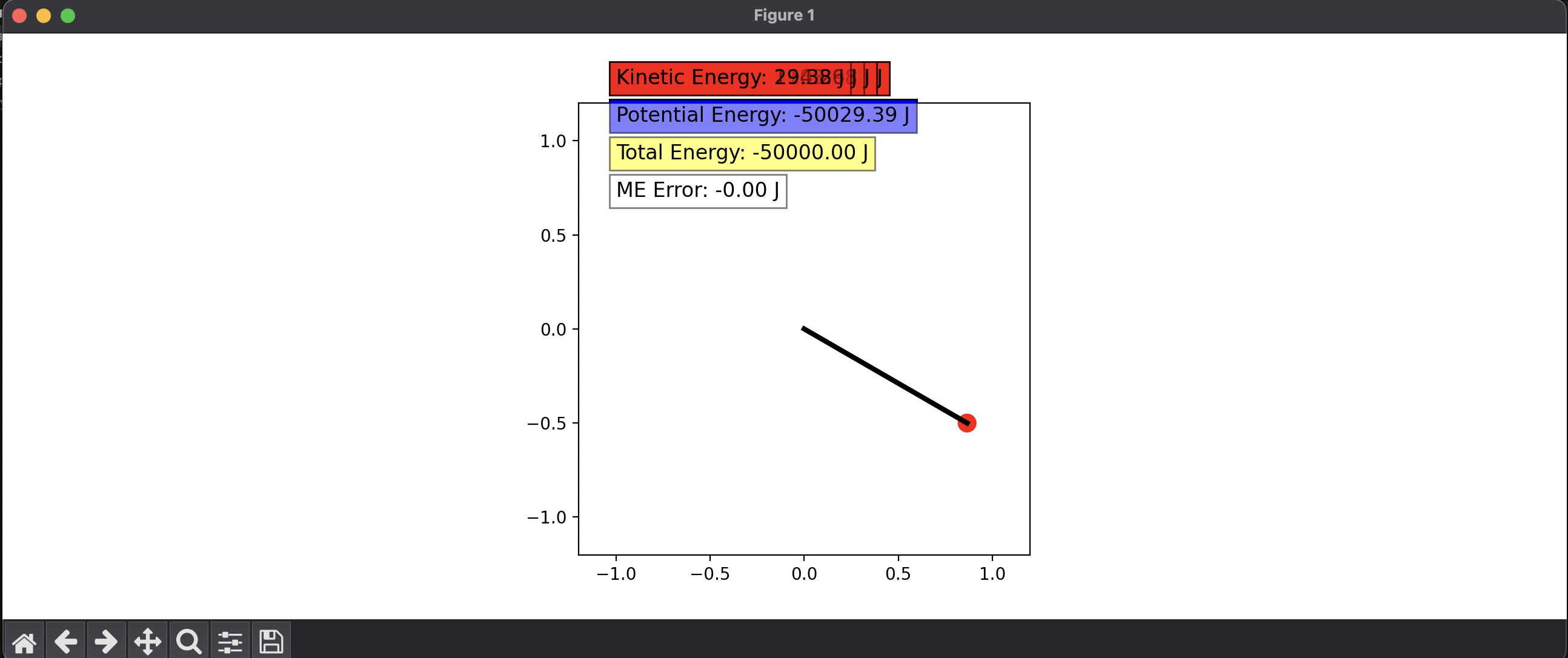
Possible Improvements

It will be useful to calculate a percent error and see how that accumulates for each of the 4 simulations. An error-time graph will also be insightful.